Morris 遍历

发表于 | 分类于 | 阅读次数

1. 二叉树遍历

树是最重要的数据结构之一，而树的遍历是树最基本的操作。

二叉树的遍历一般来说有三种遍历次序：

  • 前序遍历
  • 中序遍历
  • 后序遍历

而这三种遍历次序都可以采用递归和非递归的方式来完成。

就时间、空间的复杂度来讲，因为非递归需要借助额外的Stack来完成操作，所以递归和非递归的时间复杂度都是O(n)，O(logn)。

那么有没有另外的不同的二叉树遍历方法，在时间或空间能做到更优的呢？答案是：Morris 遍历。

由于在遍历的时候，我们需要记住某种遍历次序的的后驱或者前驱结点，常见的递归和非递归都是采用栈的方式完成这个过程，有没有内部空间来记录这些后驱或者前驱结点呢？有，那就是叶结点的左，右孩子结点，因为叶结点的两个孩子结点都是空指针，如果利用好这些空间，我们就可以在O(1) 的空间完成遍历。

利用叶结点的左、右孩子指向遍历的前驱或者后驱结点，这些指针叫做线索，对应的二叉树叫做线索二叉树。

Morris遍历是使用线索二叉树进行中序遍历的一种实现，其可以在O(n)的时间，O(1)的空间完成遍历， 对其稍加修改可以推广到先序、后序遍历，其遍历过程包含三个部分：

  1. 创建指向中序后驱结点的线索；
  2. 遍历输出结点；
  3. 删除线索，恢复树的结构；

2. Morris 中序遍历

Morris 中序遍历过程如下：

  1. 当前结点的左孩子是否为空，若是则输出当前结点，更当前结点为当前结点的右孩子；否则进入2；

  2. 在当前结点的左子树中寻找中序遍历下的前驱结点（左子树中最右结点）

    a. 若前驱结点的右孩子为空，则将前驱结点的右孩子指向当前结点，当前结点更新为当前结点的左孩子；进入3；

    b. 若前驱结点的右孩子为当前结点（不为空），将前驱结点的右孩子置NULL，输出当前结点，当前结点更新为当前结点的右孩子，进入3；

  3. 若当前结点不为空，进入1；否则程序结束；

伪代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
cur = root
repeat until cur != NULL:
	if cur.left != NULL:
		pre = cur.left;
		while pre.right == NULL && pre.right != cur://找到前驱结点pre
			pre = pre.right
		if pre.right == NULL:
			pre.right = cur
			cur = cur.left
		else:
			print(cur)
			pre.right = NULL
			cur = cur.right
	else:
		print(cur)
		cur = cur.right

下图为每一步迭代的结果（从左至右，从上到下），cur代表当前节点，深色节点表示该节点已输出。

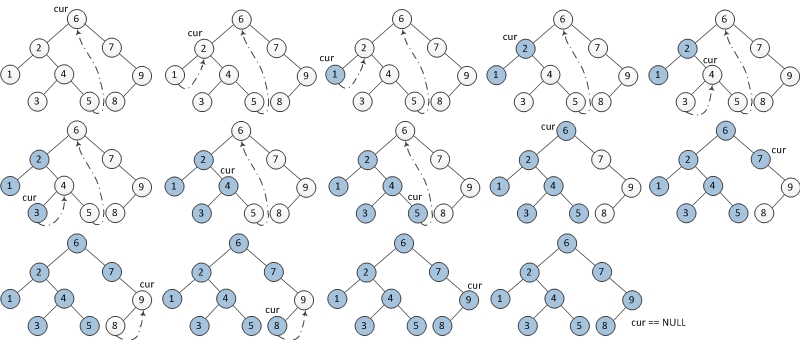
以下为Java的实现:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
public static void inOrder(TreeNode root) {
	TreeNode cur = root, pre = null;
	for (; cur != null;) {
		if (cur.left != null) {
			pre = cur.left;
			// find predecessor
			while (pre.right != null && pre.right != cur)
				pre = pre.right;
			if (pre.right == null) {// create thread
				pre.right = cur;
				cur = cur.left;
			} else {
				print(cur);
				pre.right = null;
				cur = cur.right;
			}
		} else {
			print(cur);
			cur = cur.right;
		}
	}
}

3. Morris 前序遍历

对于前序遍历，只需要在中序遍历的基础上稍加修改便可以完成。

Morris 前序遍历的流程如下：

  1. 当前结点的左孩子是否为空，若是则输出当前结点，并更新当前结点为当前结点的右孩子；否则进入2；

  2. 在当前结点的左子树中寻找中序遍历下的前驱结点（左子树中最右结点）

    a. 若前驱结点的右孩子为空，则将前驱结点的右孩子指向当前结点，输出当前结点（在这里输出，和中序遍历不同的地方），当前结点更新为当前结点的左孩子；进入3；

    b. 若前驱结点的右孩子为当前结点（不为空），将前驱结点的右孩子置NULL，当前结点更新为当前结点的右孩子，进入3；

  3. 若当前结点不为空，进入1；否则程序结束；

伪代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
cur = root;
repeat until cur != NULL:
	if cur.left != NULL:
		pre = cur.left;
		while pre.right == NULL && pre.right != cur://找到前驱结点pre
			pre = pre.right
		if pre.right == NULL:
			pre.right = cur
			print(cur)//此处和中序遍历不同
			cur = cur.left
		else:
			pre.right = NULL
			cur = cur.right
	else:
		print(cur)
		cur = cur.right

下图为每一步迭代的结果（从左至右，从上到下），cur代表当前节点，深色节点表示该节点已输出。

以下为Java的实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
public static void preOrder(TreeNode root) {
	TreeNode cur = root, pre = null;
	for (;cur != null;) {
		if (cur.left != null) {
			pre = cur.left;
			// find predecessor
			while (pre.right != null && pre.right != cur)
				pre = pre.right;
			if (pre.right == null) {// create thread
				print(cur);// print node here 
				pre.right = cur;
				cur = cur.left;
			} else {
				pre.right = null;//delete thread
				cur = cur.right;
			}
		} else {
			print(cur);
			cur = cur.right;
		}
	}
}

4. Morris 后序遍历

后序遍历的流程如下：

  1. 新建一个Dummy结点，该结点的左孩子指向树根root，将Dummy作为当前结点；

  2. 当前结点的左孩子是否为空，更新当前结点为当前结点的右孩子；否则进入2；

  3. 在当前结点的左子树中寻找中序遍历下的前驱结点（左子树中最右结点）：

    a. 若前驱结点的右孩子为空，则将前驱结点的右孩子指向当前结点，当前结点更新为当前结点的左孩子，进入3；

    b. 若前驱结点的右孩子为当前结点（不为空），反转当前结点到前驱结点之间的路径，输出该路径所有结点；反转当前结点到前驱结点之间的路径，恢复原状。将前驱结点的右孩子置NULL，当前结点更新为当前结点的右孩子，进入3；

  4. 若当前结点不为空，进入1；否则程序结束；

伪代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
dummy = Node(-1)
dummy.left = root
cur = dummy
repeat until cur != NULL:
	if cur.left != NULL:
		pre = cur.left;
		while pre.right == NULL && pre.right != cur://找到前驱结点pre
			pre = pre.right
		if pre.right == NULL:
			pre.right = cur
			cur = cur.left
		else:
			reverse(cur.left, pre)
			print(pre, cur.left)
			reverse(pre, cur.left)//再次反转，恢复原状
			pre.right = NULL
			cur = cur.right
	else:
		cur = cur.right

下图为每一步迭代的结果（从左至右，从上到下），cur代表当前节点，深色节点表示该节点已输出。

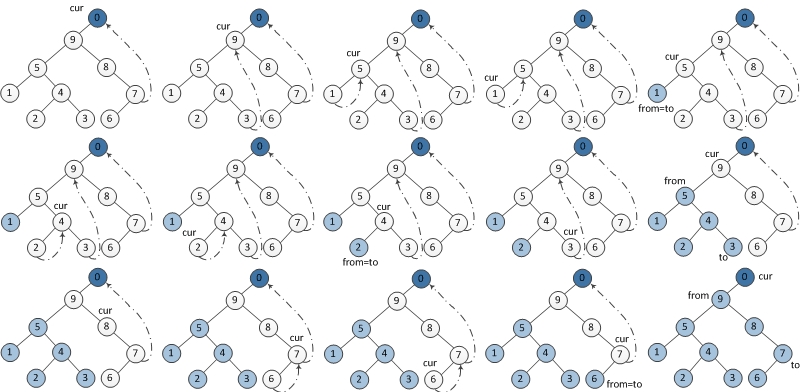
以下为Java的实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
public static void postOrder(TreeNode root) {
		// TODO Auto-generated method stub
		TreeNode dummy = new TreeNode(-1);
		dummy.left = root;
		TreeNode cur = dummy, pre = null;
		for (;cur != null;) {
			if (cur.left != null) {
				pre = cur.left;
				// find predecessor
				while (pre.right != null && pre.right != cur)
					pre = pre.right;
				if (pre.right == null) {// create thread
					pre.right = cur;
					cur = cur.left;
				} else {//print here
					reverse(cur.left, pre);
					print(pre, cur.left);
					reverse(pre, cur.left);
					pre.right = null;
					cur = cur.right;
				}
				
			} else {
				cur = cur.right;
			}
		}
	}

	private static void print(TreeNode from, TreeNode to) {
		// TODO Auto-generated method stub
		for (;;from = from.right) {
			print(from);
			if (from == to) break;
		}
	}

	private static void reverse(TreeNode from, TreeNode to) {
		// TODO Auto-generated method stub
		if (from == to) return;
		TreeNode x = from, y = from.right, z= null;
		x.right = null;
		for (;;) {
			z = y.right;
			y.right = x;
			x = y;
			if (y == to) break;
			y = z;
		}
	}

完整的代码：详见

https://github.com/Spground/archive/blob/master/misc/code/MorrisTraversalDemo.java

5. References

  1. http://www.cnblogs.com/AnnieKim/archive/2013/06/15/MorrisTraversal.html
  2. https://en.wikipedia.org/wiki/Tree_traversal#Morris_in-order_traversal_using_threading
  3. https://en.wikipedia.org/wiki/Threaded_binary_tree#The_array_of_Inorder_traversal